Random Number Generation

RNG

Randomness in Pokemon Emerald (and all other pokemon games) is not truly random. For Emerald, they used a pseudo-random number generator (pRNG or RNG) to fake randomness. The RNG algorithm they used is a linear congruential generator, given by Equation \eqref{equ:rng} where $\text{seed}_0=0$.

\begin{equation} \label{equ:rng} \text{seed}_{n+1} = \text{seed}_n \times \texttt{0x41C64E6D} + \texttt{0x6073} \end{equation}

The current seed value is stored at memory address $\texttt{0x03005D80}$ on the System Bus as a 32 bit unsigned integer (uint_32). The number of times RNG has been advanced is located at $\texttt{0x020249C0}$ on the system bus as a uint_32. In Equation \eqref{equ:rng}, it should be observed that the seeds quickly exceed the uint_32 limit ($2^{32}\approx 4.3\times10^9$), however, any seed $>2^{32}$ will overflow, leading to Equation \eqref{equ:rng_mod}, where "mod" is the modulus operation.

\begin{equation} \label{equ:rng_mod} \text{seed}_{n+1} \equiv \text{seed}_n \times \texttt{0x41C64E6D} + \texttt{0x6073} \pmod{2^{32}} \end{equation}

It can be useful to calculate $\text{seed}_{n-1}$ from $\text{seed}_n$, which is given in Equation \eqref{equ:rng_inv}. The following equations make use of the Extended Euclidean algorithm and follow the steps from Matthew Bolan

\begin{align*} \text{seed}_{n} \equiv \text{seed}_{n-1} \times \texttt{0x41C64E6D} + \texttt{0x6073} &\pmod{2^{32}}\\ \text{seed}_{n}-\texttt{0x6073} \equiv \text{seed}_{n-1} \times \texttt{0x41C64E6D} &\pmod{2^{32}}\\ \texttt{0x41C64E6D}\times\texttt{0xEEB9EB65} \equiv 1 &\pmod{2^{32}}\\ \text{seed}_{n-1} \times \texttt{0x41C64E6D}\times\texttt{0xEEB9EB65}\equiv \text{seed}_{n-1} \equiv \texttt{0xEEB9EB65}\left(\text{seed}_{n}-\texttt{0x6073}\right) &\pmod{2^{32}}\\ \texttt{0xEEB9EB65} \times -\texttt{0x6073} \equiv \texttt{0xA3561A1}&\pmod{2^{32}} \end{align*} \begin{equation} \label{equ:rng_inv} \text{seed}_{n-1} \equiv \text{seed}_n\times \texttt{0xEEB9EB65} + \texttt{0xA3561A1} \pmod{2^{32}} \end{equation}

Pickup

Pickup is an ability of Zigzagoon and Linoone that, once a battle is won, $10\%$ of the time, a random item (shown below) is selected. The ability does not activate if you caught a Pokemon.

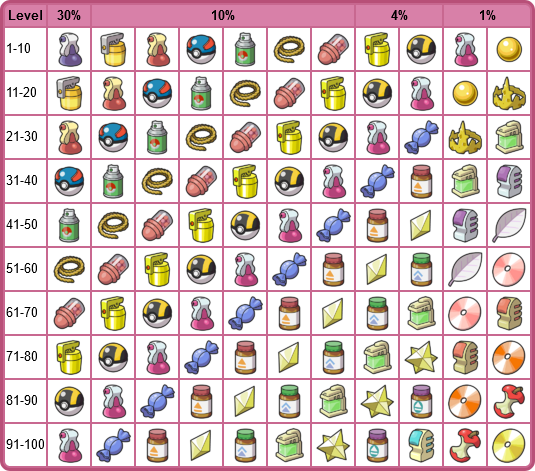
The table shows that we will start getting rare candies at level 21, having a $4\%$ chance of being the item (after the $10\%$ chance of activating pickup). It caps out at $10\%$ at level 41.

The table is not actually how the game determines the item, however. Instead, there are 2 list of items available for pickup, the regular list and a special list. The special list only determines items in the $1\%$ slots, and since rare candies are not in that list, we will be ignoring it.

Below are the items in the list.

0. Potion
1. Antidote
2. Super Potion
3. Great Ball
4. Repel
5. Escape Rope
6. X Attack
7. Full Heal
8. Ultra Ball
9. Hyper Potion
10. Rare Candy
11. Protein
12. Revive
13. HP Up
14. Full Restore
15. Max Revive
16. PP Up
17. Max Elixir

In order to determine what items are available for pickup, Equation \eqref{equ:pickup-slot} is used, where $\texttt{LVL}$ is the level of the pokemon and $i$ is the index of the first pickup item. The items in index $\in[i, i+8]$ will be used for pickup. This shifting of the indices is what causes the striping on the pickup chart above.

\begin{equation} \label{equ:pickup-slot} i = \left \lfloor{\texttt{LVL} - 1 \over 10}\right \rfloor \end{equation}

Each item does not have an equal chance (unfortunately). To determine the probabilities, ignoring the special items, the following array is used:

0. 30
1. 40
2. 50
3. 60
4. 70
5. 80
6. 90
7. 94
8. 98

Each element determines the probabilities for that index to be selected. For example, if your random number is 42 (how we will determine what this random number will be is discussed here), the game will check if 42 is less than 30, then less than, 40, and the less than 50. It is, so the game selects index 2. If the Pokemon was level 13, the item that would be selected would be the Great Ball.

Pickup Logic

When the pickup gets checked (see here for how to determine when), for each Pokemon in your party who has the ability pickup AND is not holding an item, the follow steps are done:

1. A new RNG value is calculated
2. If the upper 16 bits of the number is divisible by 10, continue, else, stop
3. A new RNG value is then calculated
4. The upper 16 bits of the RNG value mod 100 determines what item is chosen (see above)

            
                seed = rng()
                if (seed << 16) % 10 == 0:
                    itemSlot = (rng() << 16) % 100
                    item = determineItem(itemSlot, monLevel)
            
        

It should also be noted that, when in a battle, the RNG cycles 2 times per frame.

When Pickup happens

Unfortunately, it it not easy to determine what the frame pickup will happen. It does happen about 50 frames after your last input (usually "mon gained xp" for wild battles and "trainer gave you money" text boxes).

The best way I have found is to close the last text box, wait until RNG cycles more than 2 times in a frame (the only extraneous RNG calls during this time will be pickup), and calculate the difference. It's not the most elegant solution, but it works.

Expected Time

Now it's time for probability. The probability $p$ that, on 1 frame, with $m$ pickup pokemon (for the rest of this discussion, I will be dropping the "pickup" adjective), each with a probability of $p_{RC}$ of selecting a Rare Candy, to get at-least $n$ rare candies is described in Equation \eqref{equ:pickup_prob}.

\begin{equation} \label{equ:pickup_prob} p(m,n,p_{RC}) = {{m}\choose{n}}\times(0.1\times p_{RC}) \end{equation}

So if you want 2 rare candies from a party of 5 level 21-40 linoone:

$$p(5,2,0.04)={5\choose2}(0.1\times0.04)^2=1.6\times10^{-4}$$

Since $p$ is per frame, and we get to choose when to trigger pickup, we can get as many rare candies as we want. However, the probability of finding extra rare candies drops of exponentially. To determine the probability $p_D$ of finding rare candies within $D$ frames, Equation \eqref{equ:pickup_prob_time} is used.

\begin{equation} \label{equ:pickup_prob_time} p_D = 1-\left(1-p(m,n,p_{RC})\right)^D \end{equation}

You do not want to delay too long because you would be able to start another battle and get the 1 or 2 quick rare candies. So how long should we wait? First lets find the expected delay for 1-6 rare candies. Firstly, we must convert $P_D$, with some $p(m,n,p_{RC})=p$, for a probability density function and then use the expected value formula to calculate the expected value $E(D)$

\begin{align*} P_{x}(D) &= \begin{cases} p_D(0) & D=0\\ P_D(D)-P_D(D-1) & D>0 \end{cases}\\ E(D) &= \sum_{d=0}^\infty dP_{x} = P_D(0) + \sum_{d=1}^\infty d\left( P_D(d)-P_D(d-1) \right)\\ &= P_D(0) + \sum_{d=1}^\infty d\left( 1-\left(1-p\right)^d-1+\left(1-p\right)^{d-1} \right)\\ &= P_D(0) + \sum_{d=1}^\infty d\left( \left(1-p\right)^{d-1}-\left(1-p\right)^d \right)\\ &=P_D(0) + (1-p)^0 - (1-p)^1 + 2(1-p)^1 - 2(1-p)^2 + 3(1-p)^2 - 3(1-p)^3+ \dots\\ &=P_D(0) + (1-p)^0 \cancel{- (1-p)^1} + \cancelto{1}{2}(1-p)^1 \cancel{- 2(1-p)^2} + \cancelto{1}{3}(1-p)^2 \cancel{- 3(1-p)^3} +\dots\\ &=P_D(0) + (1-p)^0 + (1-p)^1 + (1-p)^2 + (1-p)^3 + \dots\\ E(D) &=P_D(0) + \sum_{d=0}^\infty (1-p)^d \end{align*}

We know that $(1-p) < 1$, so we are able to use the geometric series convergence formula, Equation \eqref{equ:geom}, which lets us find $E(D)$ using Equation \eqref{equ:d_expect} (this is probably some well known formula that I'm forgetting about).

\begin{align} \label{equ:geom} \sum ar^k = {a \over 1-r} \end{align} \begin{align*} E(D) &= P_D(0) + \sum_{d=0}^\infty (1-p)^d = P_D(0) + {1\over 1-(1-p)} = P_D(0) + {1\over p}\\ &= 1-\left(1-p\right)^0 + {1\over p} = 1-1+{1\over p} \end{align*} \begin{equation} \label{equ:d_expect} E(D) = {1\over p} \end{equation}

Below is a table for parties of 5 Pokemon that are either level 21-40 or 41+ for the expected number of frames you would need to wait.

Number of Rare Candies	$E(D)$ Level $\in[21,40]$ (frames)	$E(D)$ Level $\ge 41$ (frames)
$0$	$1$	$1$
$1$	$50$	$20$
$2$	$6250$	$1000$
$3$	$1.56\times 10^6$	$1.0\times 10^{5}$
$4$	$7.81\times 10^8$	$2.0\times 10^{7}$
$5$	$9.77\times 10^{11}$	$1.0\times 10^{10}$

The table shows that you are expected to get no rare candies in 1 frame (which makes sense) and after 2 rare candies, it would take significantly longer to wait for extra candies than just doing another battle.